Factoring Binomials Raised to a Power of n January, 2008
Factoring binomials raised to a particular power can be done easily when you follow a few patterns. We'll use the following binomial to demonstrate these patterns: (2a - b)3. I'm going to do this the long way to illustrate the mechanics.
The first pattern has to do with the power the binomial is raised to. The factored form will first have the original terms multiplied by each other to form a new term. This new term will be added to itself the same number of times as the power of the unfactored binomial plus one; in this example it will be 4 (3 + 1). Since the operation in the unfactored binomial is subtraction the second term, b, will be negative.
(2a)(-b) + (2a)(-b) + (2a)(-b) + (2a)(-b)
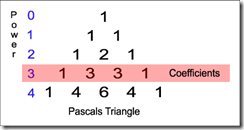
The next pattern involves the coefficients. The coefficients for each term in the factored binomial match a row in Pascal's Triangle. The row number we want in Pascal's Triangle is the power the unfactored binomial was raised too (With the first row in the triangle being zero). So in this example the binomial is raised to the 3rd power and the coefficients will match the values in row 3 of Pascal's Triangle: 1, 3, 3 and 1 in that order.
1(2a)(-b) + 3(2a)(-b) + 3(2a)(-b) + 1(2a)(-b)
The next pattern involves the powers of the terms. The first term in the original unfactored binomial, 2a, starts with the power of the original unfactored binomial and decreases by one, in the factored form. The second term in the original unfactored binomial, b, starts with a power of zero and increases by one, in the factored form.
1(2a)3(-b)0 + 3(2a)2(-b)1 + 3(2a)1(-b)2 + 1(2a)0(-b)3
Now the factored form can be reduced. First, if the terms in the unfactored binomial are subtracted, every other operation in the factored binomial will be subtraction. This occurs because the power determines the sign of the term. Negative terms raised to an even number will be positive (IE: -22 == -2 * -2 == 4) and negative terms raised to an odd power will remain negative (IE: -23 == -2 * -2 * -2 == -8). The pattern ends up being the first first operation is subtraction, the second is addition and so on.
1(2a)3(b)0 - 3(2a)2(b)1 + 3(2a)1(b)2 - 1(2a)0(b)3
Now reduce the terms:
8a3 - 12a2b + 6ab2 - b3
So a binomial raised to the third power, (a + b)3, will follow this pattern:
a3 + 3a2b + 3ab2 + b3
The following script will factor out binomials (at least to a certain degree):
| ( ) |
| Unfactored | |
| Factored | |
| Reduced |

 Bender (51 )
Bender (51 )